ANUEET 2024 Download Hall Ticket ANU Engineering Entrance Test : Acharya Nagarjuna University

Organisation : Acharya Nagarjuna University
Exam Name : ANU Engineering Entrance Test-2024 ANUEET
Announcement : Download Hall Ticket
Exam Date : 15.06.2024
Website : https://www.nagarjunauniversity.ac.in/

ANU Download Hall Ticket ANUEET

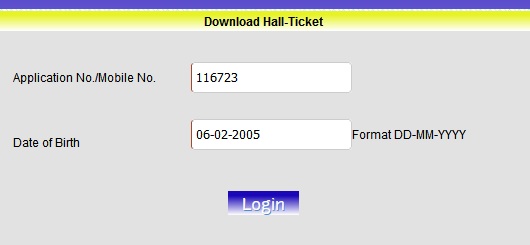
Date of Exmination will be held on 15-06-2024 (Saturday). 11.00 AM. To Download Hall Ticket for ANU Engineering Entrance Test-2024 follow the below steps
Steps :
Step-1 : Go to the link http://www.anucet.in/printhallticket.aspx
Step-2 : Enter Application No./Mobile No.
Step-3 : Enter Date of Birth Format DD-MM-YYYY
Step-4 : Click on “Login” Button.

Related / Similar Admit Card : AAU Download Admit Card 2024 CET UG Common Entrance Test Undergraduate

Syllabus For ANU Engineering Entrance Test

MATHEMATICS :
ALGEBRA :
a) Functions: Types of functions – Definitions – Real valued functions (Domain and Range).

b) Matrices: Types of matrices – Scalar multiple of a matrix and multiplication of matrices- Transpose of a matrix – Determinants (excluding properties of determinants) – Adjoint and Inverse of a matrix – Rank of a matrix – solution of simultaneous linear equations (Excluding Gauss Jordan Method).

c) Complex Numbers: Complex number as an ordered pair of real numbers fundamental operations – Representation of complex numbers in the form a+ib (excluding Square root of Complex numbers and related problems) – Modulus and amplitude of complex numbers –Illustrations – Geometrical and Polar Representation of complex numbers in Argand plane-Argand diagram.

d) De Moivre’s Theorem: De Moivre’s theorem- Integral and Rational indices – nth roots of unity Geometrical Interpretations –Illustrations.
e) Quadratic Expressions: Quadratic expressions, equations in one variable – Sign of quadratic\ expressions – Change in signs – Maximum and minimum values.

f) Theory of Equations: The relation between the roots and coefficients in an equation – Solving the equations when two or more roots of it are connected by certain relation – Equation with real coefficients, occurrence of complex roots in conjugate pairs and its consequences.

g) Permutations and Combinations: Fundamental Principle of counting – linear and circular permutations- Permutations of ‘n’ dissimilar things taken ‘r’ at a time – Permutations when repetitions allowed – Circular permutations – Permutations with constraint repetitions Combinations-definitions, certain theorems. (Excluding derivation of Formula npr and ncr ).

h) Partial fractions: Partial fractions of f(x)/g(x) when g(x) contains non –repeated linear factors Partial fractions of f(x)/g(x) where both f(x) and g(x) are polynomials and when g(x) contains repeated and/or non-repeated linear factors – Partial fractions of f(x)/g(x) when g(x) contains irreducible factors (excluding conversion of f(x)/g(x) in power series of x).

TRIGONOMETRY :
a) Trigonometric Ratios upto Transformations: Graphs and Periodicity of Trigonometric functions – Trigonometric ratios and Compound angles – Trigonometric ratios of multiple and sub- multiple angles – Transformations – Sum and Product rules.
b) Hyperbolic Functions: Definition of Hyperbolic Function – Graphs – Definition of Inverse Hyperbolic Functions – Graphs – Addition formulae of Hyperbolic Functions.
c) Properties of Triangles: Relation between sides and angles of a Triangle – Sine, Cosine, Tangent and Projection rules- Half angle formulae and areas of a triangle–In-circle and Ex-circle of a Triangle (excluding problems related to heights and distances).

VECTOR ALGEBRA :
a) Addition of Vectors: Vectors as a triad of real numbers – Classification of vectors – Addition of vectors – Scalar multiplication – Angle between two non-zero vectors – Linear combination of vectors – Component of a vector in three dimensions – Vector equations of line and plane including their Cartesian equivalent forms.

b) Product of Vectors: Scalar Product – Geometrical Interpretations – orthogonal projections Properties of dot product – Expression of dot product in i, j, k system – Angle between two vectors – Geometrical Vector methods – Vector equations of plane in normal form-Angle between two planes- Vector product of two vectors and properties- Vector product in i, j, k system – Vector Areas.

MEASURES OF DISPERSION AND PROBABILITY :
a) Measures of Dispersion – Range – Mean deviation – Variance and standard deviation of ungrouped/grouped data.
b) Probability: Random experiments and events – Classical definition of probability, Axiomatic approach and addition theorem of probability – Independent and dependent events – conditional probability- multiplication theorem and Baye’s theorem.
c) Random Variables and Probability Distributions: Random Variables – Theoretical discrete distributions – Binomial and Poisson Distributions.

ANUEET Model Question Paper

Time: 90 Min
Max. Marks: 100
The test paper consists of 3 parts. Each part contains 30 multiple choice questions. Answer all questions in each part.

Part – A: Mathematics (40 marks)
1. The variance of 30 observations is 3. If each of the observations is multiplied by 3, then the variance of the resulting observations is :
1) 3
2) 9
3) 27
4) 81

Part – B: Physics (30 marks)
2. 5 bulbs each of 100 W are connected across 220 V power supply for domestic application. If each unit costs Rs.4 then the cost per day in Rs. Is
1) 48
2) 24
3) 96
4) 12

Part – C: Chemistry (30 marks)
3. Which one of the following has stable electroniccon figuration?
1) N
2) C
3) F
4) Al